In Which Dataset Would You Most Likely See The Discharge Date As Data Element?

Multivariate Time Series Forecasting with LSTMs in Keras

Concluding Updated on October 21, 2020

Neural networks like Long Short-Term Memory (LSTM) recurrent neural networks are able to almost seamlessly model problems with multiple input variables.

This is a great benefit in time serial forecasting, where classical linear methods tin can be difficult to adapt to multivariate or multiple input forecasting problems.

In this tutorial, you will notice how you can develop an LSTM model for multivariate time series forecasting with the Keras deep learning library.

After completing this tutorial, yous will know:

How to transform a raw dataset into something nosotros tin use for fourth dimension series forecasting.
How to gear up data and fit an LSTM for a multivariate time serial forecasting problem.
How to make a forecast and rescale the upshot back into the original units.

Kick-beginning your project with my new volume Deep Learning for Time Serial Forecasting, including pace-by-step tutorials and the Python source code files for all examples.

Let's get started.

Update Aug/2017: Fixed a bug where yhat was compared to obs at the previous time step when calculating the final RMSE. Thanks, Songbin Xu and David Righart.
Update Oct/2017: Added a new example showing how to railroad train on multiple prior time steps due to popular need.
Update Sep/2018: Updated link to dataset.
Update Jun/2020: Fixed missing imports for LSTM information prep example.

Tutorial Overview

This tutorial is divided into 4 parts; they are:

Air Pollution Forecasting
Basic Data Preparation
Multivariate LSTM Forecast Model
1. LSTM Data Preparation
2. Define and Fit Model
3. Evaluate Model
4. Complete Example
Train On Multiple Lag Timesteps Example

Python Environment

This tutorial assumes you have a Python SciPy environment installed. I recommend that youuse Python 3 with this tutorial.

You must have Keras (2.0 or higher) installed with either the TensorFlow or Theano backend, Ideally Keras ii.3 and TensorFlow 2.2, or higher.

The tutorial also assumes you have scikit-learn, Pandas, NumPy and Matplotlib installed.

If you need assist with your environment, see this post:

How to Setup a Python Environment for Automobile Learning

Need help with Deep Learning for Time Series?

Take my free 7-day email crash class at present (with sample lawmaking).

Click to sign-up and also become a free PDF Ebook version of the course.

1. Air Pollution Forecasting

In this tutorial, we are going to use the Air Quality dataset.

This is a dataset that reports on the weather and the level of pollution each hr for five years at the U.s.a. embassy in Beijing, People's republic of china.

The data includes the date-fourth dimension, the pollution called PM2.5 concentration, and the weather information including dew point, temperature, pressure, current of air direction, wind speed and the cumulative number of hours of snow and rain. The complete feature list in the raw data is as follows:

No: row number
year: yr of data in this row
month: month of information in this row
day: day of data in this row
hour: hour of information in this row
pm2.5: PM2.5 concentration
DEWP: Dew Betoken
TEMP: Temperature
PRES: Pressure level
cbwd: Combined wind direction
Iws: Cumulated current of air speed
Is: Cumulated hours of snow
Ir: Cumulated hours of pelting

We tin utilize this information and frame a forecasting problem where, given the atmospheric condition weather and pollution for prior hours, we forecast the pollution at the next hr.

This dataset can be used to frame other forecasting problems.
Do y'all have good ideas? Let me know in the comments below.

Y'all can download the dataset from the UCI Machine Learning Repository.

Update, I take mirrored the dataset here because UCI has become unreliable:

Beijing PM2.5 Information Set

Download the dataset and place it in your current working directory with the filename "raw.csv".

2. Basic Information Preparation

The information is not set to use. We must prepare it first.

Below are the first few rows of the raw dataset.

No,year,month,24-hour interval,hour,pm2.5,DEWP,TEMP,PRES,cbwd,Iws,Is,Ir

i,2010,1,i,0,NA,-21,-11,1021,NW,ane.79,0,0

ii,2010,1,1,1,NA,-21,-12,1020,NW,iv.92,0,0

iii,2010,1,1,ii,NA,-21,-11,1019,NW,6.71,0,0

4,2010,ane,ane,3,NA,-21,-xiv,1019,NW,9.84,0,0

v,2010,one,i,four,NA,-20,-12,1018,NW,12.97,0,0

The first pace is to consolidate the date-time information into a single date-time and so that we tin can apply information technology as an index in Pandas.

A quick check reveals NA values for pm2.5 for the first 24 hours. We volition, therefore, need to remove the first row of data. There are also a few scattered "NA" values after in the dataset; we can mark them with 0 values for now.

The script below loads the raw dataset and parses the date-time information as the Pandas DataFrame alphabetize. The "No" column is dropped and then clearer names are specified for each column. Finally, the NA values are replaced with "0" values and the first 24 hours are removed.

The "No" column is dropped and then clearer names are specified for each column. Finally, the NA values are replaced with "0" values and the kickoff 24 hours are removed.

ane

two

half dozen

seven

xiv

from pandas import read_csv

from datetime import datetime

# load data

def parse ( x ) :

return datetime . strptime ( 10 , '%Y %thousand %d %H' )

dataset = read_csv ( 'raw.csv' , parse_dates = [ [ 'twelvemonth' , 'month' , 'day' , 'hour' ] ] , index_col = 0 , date_parser = parse )

dataset . drop ( 'No' , axis = 1 , inplace = True )

# manually specify column names

dataset . columns = [ 'pollution' , 'dew' , 'temp' , 'press' , 'wnd_dir' , 'wnd_spd' , 'snow' , 'rain' ]

dataset . index . name = 'date'

# marking all NA values with 0

dataset [ 'pollution' ] . fillna ( 0 , inplace = True )

# drop the commencement 24 hours

dataset = dataset [ 24 : ]

# summarize first five rows

impress ( dataset . head ( five ) )

# salvage to file

dataset . to_csv ( 'pollution.csv' )

Running the example prints the beginning v rows of the transformed dataset and saves the dataset to "pollution.csv".

pollution dew temp press wnd_dir wnd_spd snow rain

date

2010-01-02 00:00:00 129.0 -sixteen -4.0 1020.0 SE i.79 0 0

2010-01-02 01:00:00 148.0 -15 -4.0 1020.0 SE 2.68 0 0

2010-01-02 02:00:00 159.0 -11 -5.0 1021.0 SE 3.57 0 0

2010-01-02 03:00:00 181.0 -7 -5.0 1022.0 SE 5.36 ane 0

2010-01-02 04:00:00 138.0 -vii -5.0 1022.0 SE 6.25 two 0

Now that we take the information in an easy-to-use form, we tin can create a quick plot of each series and see what we have.

The code below loads the new "pollution.csv" file and plots each serial as a separate subplot, except wind speed dir, which is categorical.

from pandas import read_csv

from matplotlib import pyplot

# load dataset

dataset = read_csv ( 'pollution.csv' , header = 0 , index_col = 0 )

values = dataset . values

# specify columns to plot

groups = [ 0 , one , 2 , 3 , 5 , 6 , seven ]

i = 1

# plot each column

pyplot . effigy ( )

for group in groups :

pyplot . subplot ( len ( groups ) , 1 , i )

pyplot . plot ( values [ : , group ] )

pyplot . championship ( dataset . columns [ group ] , y = 0.five , loc = 'right' )

i += i

pyplot . show ( )

Running the case creates a plot with seven subplots showing the 5 years of information for each variable.

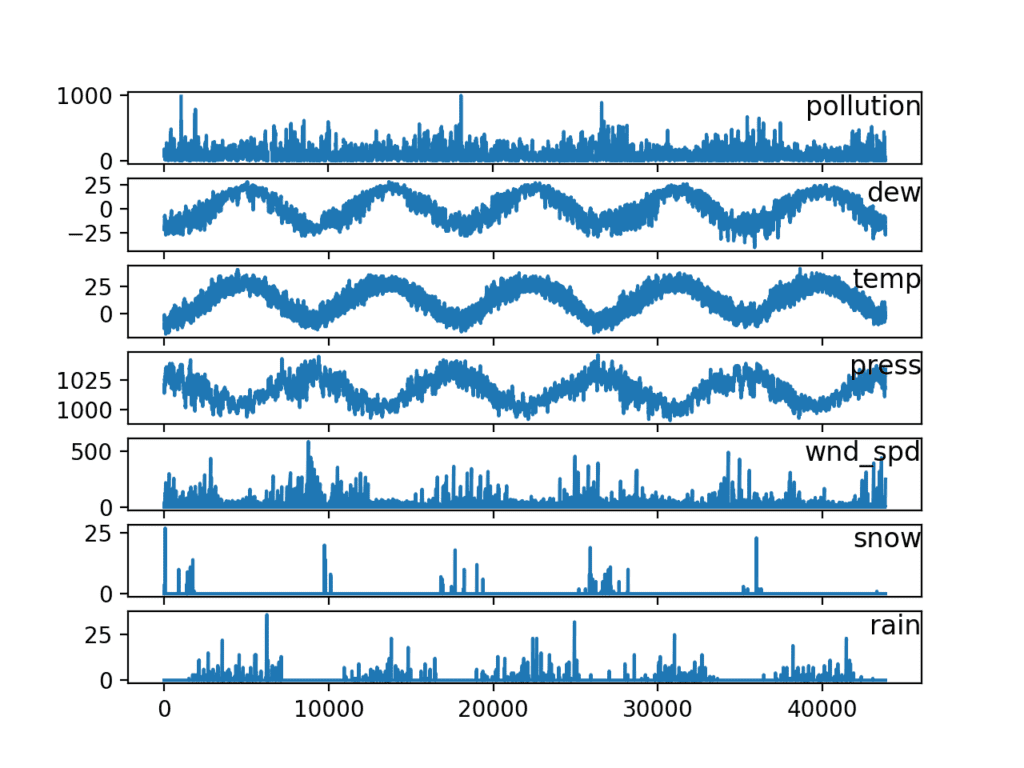
Line Plots of Air Pollution Time Serial

3. Multivariate LSTM Forecast Model

In this department, we will fit an LSTM to the problem.

LSTM Information Preparation

The showtime step is to set up the pollution dataset for the LSTM.

This involves framing the dataset as a supervised learning problem and normalizing the input variables.

We will frame the supervised learning problem equally predicting the pollution at the current hour (t) given the pollution measurement and conditions conditions at the prior time pace.

This formulation is straightforward and just for this sit-in. Some alternating formulations you could explore include:

Predict the pollution for the side by side hour based on the weather weather and pollution over the last 24 hours.
Predict the pollution for the adjacent hour equally above and given the "expected" weather conditions for the adjacent hour.

We can transform the dataset using the series_to_supervised() function developed in the weblog post:

How to Convert a Time Series to a Supervised Learning Trouble in Python

First, the "pollution.csv" dataset is loaded. The wind management feature is label encoded (integer encoded). This could further be one-hot encoded in the future if you are interested in exploring information technology.

Adjacent, all features are normalized, so the dataset is transformed into a supervised learning problem. The atmospheric condition variables for the hour to be predicted (t) are so removed.

The complete lawmaking listing is provided below.

iii

five

xiv

fifteen

nineteen

# ready data for lstm

from pandas import read_csv

from pandas import DataFrame

from pandas import concat

from sklearn . preprocessing import LabelEncoder

from sklearn . preprocessing import MinMaxScaler

# convert serial to supervised learning

def series_to_supervised ( data , n_in = 1 , n_out = 1 , dropnan = True ) :

n_vars = 1 if type ( data ) is list else data . shape [ one ]

df = DataFrame ( information )

cols , names = list ( ) , listing ( )

# input sequence (t-n, ... t-1)

for i in range ( n_in , 0 , - i ) :

cols . append ( df . shift ( i ) )

names += [ ( 'var%d(t-%d)' % ( j + 1 , i ) ) for j in range ( n_vars ) ]

# forecast sequence (t, t+1, ... t+northward)

for i in range ( 0 , n_out ) :

cols . suspend ( df . shift ( - i ) )

if i == 0 :

names += [ ( 'var%d(t)' % ( j + 1 ) ) for j in range ( n_vars ) ]

else :

names += [ ( 'var%d(t+%d)' % ( j + 1 , i ) ) for j in range ( n_vars ) ]

# put information technology all together

agg = concat ( cols , axis = i )

agg . columns = names

# drib rows with NaN values

if dropnan :

agg . dropna ( inplace = True )

render agg

# load dataset

dataset = read_csv ( 'pollution.csv' , header = 0 , index_col = 0 )

values = dataset . values

# integer encode direction

encoder = LabelEncoder ( )

values [ : , 4 ] = encoder . fit_transform ( values [ : , 4 ] )

# ensure all data is bladder

values = values . astype ( 'float32' )

# normalize features

scaler = MinMaxScaler ( feature_range = ( 0 , 1 ) )

scaled = scaler . fit_transform ( values )

# frame as supervised learning

reframed = series_to_supervised ( scaled , ane , 1 )

# driblet columns we don't want to predict

reframed . drop ( reframed . columns [ [ nine , 10 , eleven , 12 , thirteen , fourteen , fifteen ] ] , centrality = 1 , inplace = True )

impress ( reframed . head ( ) )

Running the example prints the outset v rows of the transformed dataset. We can run across the 8 input variables (input serial) and the 1 output variable (pollution level at the current hour).

var1(t-1) var2(t-1) var3(t-1) var4(t-i) var5(t-one) var6(t-1) \

one 0.129779 0.352941 0.245902 0.527273 0.666667 0.002290

two 0.148893 0.367647 0.245902 0.527273 0.666667 0.003811

3 0.159960 0.426471 0.229508 0.545454 0.666667 0.005332

4 0.182093 0.485294 0.229508 0.563637 0.666667 0.008391

5 0.138833 0.485294 0.229508 0.563637 0.666667 0.009912

var7(t-1) var8(t-1) var1(t)

i 0.000000 0.0 0.148893

ii 0.000000 0.0 0.159960

three 0.000000 0.0 0.182093

4 0.037037 0.0 0.138833

v 0.074074 0.0 0.109658

This data preparation is unproblematic and there is more we could explore. Some ideas you could look at include:

One-hot encoding wind management.
Making all series stationary with differencing and seasonal adjustment.
Providing more i hour of input fourth dimension steps.

This last point is perhaps the most important given the use of Backpropagation through fourth dimension by LSTMs when learning sequence prediction problems.

Define and Fit Model

In this section, we will fit an LSTM on the multivariate input data.

First, we must split the prepared dataset into train and examination sets. To speed up the training of the model for this demonstration, we will but fit the model on the first year of information, then evaluate it on the remaining iv years of data. If you accept fourth dimension, consider exploring the inverted version of this test harness.

The example beneath splits the dataset into train and test sets, and so splits the train and examination sets into input and output variables. Finally, the inputs (X) are reshaped into the 3D format expected past LSTMs, namely [samples, timesteps, features].

. . .

# split into train and test sets

values = reframed . values

n_train_hours = 365 * 24

train = values [ : n_train_hours , : ]

test = values [ n_train_hours : , : ]

# split into input and outputs

train_X , train_y = train [ : , : - ane ] , train [ : , - 1 ]

test_X , test_y = test [ : , : - 1 ] , examination [ : , - ane ]

# reshape input to be 3D [samples, timesteps, features]

train_X = train_X . reshape ( ( train_X . shape [ 0 ] , one , train_X . shape [ 1 ] ) )

test_X = test_X . reshape ( ( test_X . shape [ 0 ] , 1 , test_X . shape [ one ] ) )

print ( train_X . shape , train_y . shape , test_X . shape , test_y . shape )

Running this example prints the shape of the train and test input and output sets with nearly 9K hours of information for grooming and nigh 35K hours for testing.

(8760, one, 8) (8760,) (35039, i, eight) (35039,)

Now we can define and fit our LSTM model.

We will define the LSTM with fifty neurons in the first hidden layer and 1 neuron in the output layer for predicting pollution. The input shape volition exist i time step with 8 features.

We will utilize the Mean Accented Error (MAE) loss function and the efficient Adam version of stochastic slope descent.

The model will be fit for 50 training epochs with a batch size of 72. Remember that the internal state of the LSTM in Keras is reset at the finish of each batch, then an internal state that is a role of a number of days may exist helpful (attempt testing this).

Finally, nosotros continue runway of both the preparation and test loss during training by setting the validation_data statement in the fit() role. At the end of the run both the preparation and test loss are plotted.

. . .

# design network

model = Sequential ( )

model . add together ( LSTM ( 50 , input_shape = ( train_X . shape [ ane ] , train_X . shape [ ii ] ) ) )

model . add together ( Dense ( one ) )

model . compile ( loss = 'mae' , optimizer = 'adam' )

# fit network

history = model . fit ( train_X , train_y , epochs = l , batch_size = 72 , validation_data = ( test_X , test_y ) , verbose = 2 , shuffle = False )

# plot history

pyplot . plot ( history . history [ 'loss' ] , label = 'train' )

pyplot . plot ( history . history [ 'val_loss' ] , label = 'examination' )

pyplot . legend ( )

pyplot . evidence ( )

Evaluate Model

After the model is fit, we can forecast for the entire exam dataset.

We combine the forecast with the test dataset and capsize the scaling. We also capsize scaling on the test dataset with the expected pollution numbers.

With forecasts and actual values in their original scale, we tin then calculate an mistake score for the model. In this case, nosotros calculate the Root Hateful Squared Fault (RMSE) that gives error in the same units as the variable itself.

. . .

# make a prediction

yhat = model . predict ( test_X )

test_X = test_X . reshape ( ( test_X . shape [ 0 ] , test_X . shape [ 2 ] ) )

# invert scaling for forecast

inv_yhat = concatenate ( ( yhat , test_X [ : , 1 : ] ) , centrality = 1 )

inv_yhat = scaler . inverse_transform ( inv_yhat )

inv_yhat = inv_yhat [ : , 0 ]

# invert scaling for bodily

test_y = test_y . reshape ( ( len ( test_y ) , 1 ) )

inv_y = concatenate ( ( test_y , test_X [ : , ane : ] ) , centrality = one )

inv_y = scaler . inverse_transform ( inv_y )

inv_y = inv_y [ : , 0 ]

# summate RMSE

rmse = sqrt ( mean_squared_error ( inv_y , inv_yhat ) )

print ( 'Examination RMSE: %.3f' % rmse )

Consummate Example

The complete case is listed below.

Annotation: This instance assumes you lot have prepared the data correctly, due east.g. converted the downloaded "raw.csv" to the prepared "pollution.csv". Run across the starting time part of this tutorial.

five

six

vii

nine

thirteen

xvi

xviii

nineteen

thirty

twoscore

from math import sqrt

from numpy import concatenate

from matplotlib import pyplot

from pandas import read_csv

from pandas import DataFrame

from pandas import concat

from sklearn . preprocessing import MinMaxScaler

from sklearn . preprocessing import LabelEncoder

from sklearn . metrics import mean_squared_error

from keras . models import Sequential

from keras . layers import Dumbo

from keras . layers import LSTM

# convert series to supervised learning

def series_to_supervised ( information , n_in = 1 , n_out = 1 , dropnan = True ) :

n_vars = 1 if type ( data ) is listing else data . shape [ 1 ]

df = DataFrame ( data )

cols , names = list ( ) , list ( )

# input sequence (t-north, ... t-1)

for i in range ( n_in , 0 , - 1 ) :

cols . suspend ( df . shift ( i ) )

names += [ ( 'var%d(t-%d)' % ( j + 1 , i ) ) for j in range ( n_vars ) ]

# forecast sequence (t, t+ane, ... t+n)

for i in range ( 0 , n_out ) :

cols . append ( df . shift ( - i ) )

if i == 0 :

names += [ ( 'var%d(t)' % ( j + 1 ) ) for j in range ( n_vars ) ]

else :

names += [ ( 'var%d(t+%d)' % ( j + ane , i ) ) for j in range ( n_vars ) ]

# put it all together

agg = concat ( cols , axis = 1 )

agg . columns = names

# drib rows with NaN values

if dropnan :

agg . dropna ( inplace = True )

render agg

# load dataset

dataset = read_csv ( 'pollution.csv' , header = 0 , index_col = 0 )

values = dataset . values

# integer encode management

encoder = LabelEncoder ( )

values [ : , 4 ] = encoder . fit_transform ( values [ : , four ] )

# ensure all information is float

values = values . astype ( 'float32' )

# normalize features

scaler = MinMaxScaler ( feature_range = ( 0 , 1 ) )

scaled = scaler . fit_transform ( values )

# frame as supervised learning

reframed = series_to_supervised ( scaled , one , 1 )

# driblet columns nosotros don't want to predict

reframed . drop ( reframed . columns [ [ 9 , 10 , 11 , 12 , xiii , fourteen , 15 ] ] , axis = 1 , inplace = True )

print ( reframed . head ( ) )

# split into railroad train and exam sets

values = reframed . values

n_train_hours = 365 * 24

train = values [ : n_train_hours , : ]

exam = values [ n_train_hours : , : ]

# split into input and outputs

train_X , train_y = railroad train [ : , : - one ] , train [ : , - 1 ]

test_X , test_y = exam [ : , : - i ] , test [ : , - 1 ]

# reshape input to be 3D [samples, timesteps, features]

train_X = train_X . reshape ( ( train_X . shape [ 0 ] , 1 , train_X . shape [ 1 ] ) )

test_X = test_X . reshape ( ( test_X . shape [ 0 ] , i , test_X . shape [ one ] ) )

print ( train_X . shape , train_y . shape , test_X . shape , test_y . shape )

# design network

model = Sequential ( )

model . add ( LSTM ( fifty , input_shape = ( train_X . shape [ i ] , train_X . shape [ 2 ] ) ) )

model . add ( Dense ( 1 ) )

model . compile ( loss = 'mae' , optimizer = 'adam' )

# fit network

history = model . fit ( train_X , train_y , epochs = l , batch_size = 72 , validation_data = ( test_X , test_y ) , verbose = 2 , shuffle = False )

# plot history

pyplot . plot ( history . history [ 'loss' ] , label = 'train' )

pyplot . plot ( history . history [ 'val_loss' ] , label = 'test' )

pyplot . legend ( )

pyplot . evidence ( )

# make a prediction

yhat = model . predict ( test_X )

test_X = test_X . reshape ( ( test_X . shape [ 0 ] , test_X . shape [ 2 ] ) )

# invert scaling for forecast

inv_yhat = concatenate ( ( yhat , test_X [ : , 1 : ] ) , axis = one )

inv_yhat = scaler . inverse_transform ( inv_yhat )

inv_yhat = inv_yhat [ : , 0 ]

# invert scaling for actual

test_y = test_y . reshape ( ( len ( test_y ) , 1 ) )

inv_y = concatenate ( ( test_y , test_X [ : , 1 : ] ) , centrality = 1 )

inv_y = scaler . inverse_transform ( inv_y )

inv_y = inv_y [ : , 0 ]

# calculate RMSE

rmse = sqrt ( mean_squared_error ( inv_y , inv_yhat ) )

print ( 'Test RMSE: %.3f' % rmse )

Running the instance first creates a plot showing the train and test loss during preparation.

Notation: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the boilerplate effect.

Interestingly, we can see that test loss drops below training loss. The model may be overfitting the training data. Measuring and plotting RMSE during training may shed more light on this.

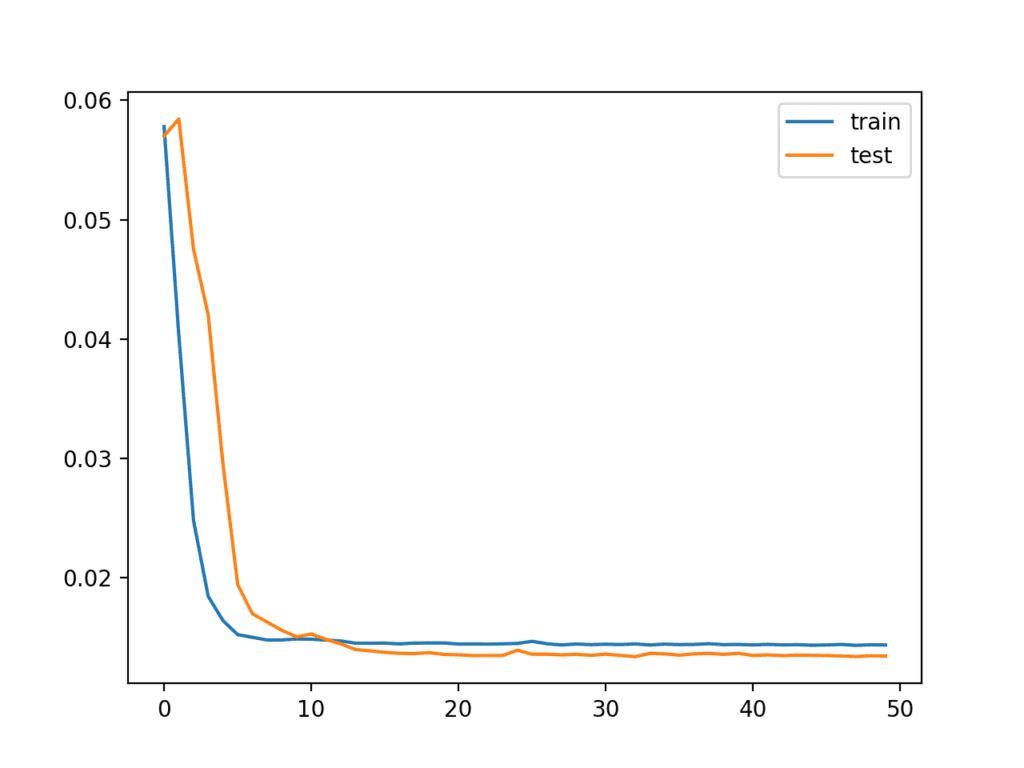
Line Plot of Train and Examination Loss from the Multivariate LSTM During Training

The Train and test loss are printed at the terminate of each training epoch. At the stop of the run, the final RMSE of the model on the test dataset is printed.

Nosotros can see that the model achieves a respectable RMSE of 26.496, which is lower than an RMSE of thirty found with a persistence model.

...

Epoch 46/50

0s - loss: 0.0143 - val_loss: 0.0133

Epoch 47/l

0s - loss: 0.0143 - val_loss: 0.0133

Epoch 48/50

0s - loss: 0.0144 - val_loss: 0.0133

Epoch 49/50

0s - loss: 0.0143 - val_loss: 0.0133

Epoch fifty/50

0s - loss: 0.0144 - val_loss: 0.0133

Test RMSE: 26.496

This model is non tuned. Tin you do better?
Allow me know your trouble framing, model configuration, and RMSE in the comments beneath.

Railroad train On Multiple Lag Timesteps Example

At that place have been many requests for communication on how to adjust the above example to train the model on multiple previous time steps.

I had tried this and a myriad of other configurations when writing the original post and decided not to include them because they did not lift model skill.

All the same, I accept included this example below every bit reference template that y'all could adapt for your own problems.

The changes needed to railroad train the model on multiple previous time steps are quite minimal, equally follows:

First, you must frame the problem suitably when calling series_to_supervised(). We volition utilize 3 hours of data as input. Also annotation, we no longer explictly drop the columns from all of the other fields at ob(t).

. . .

# specify the number of lag hours

n_hours = 3

n_features = 8

# frame as supervised learning

reframed = series_to_supervised ( scaled , n_hours , i )

Next, nosotros need to be more conscientious in specifying the column for input and output.

We have iii * 8 + 8 columns in our framed dataset. We will take 3 * 8 or 24 columns as input for the obs of all features across the previous 3 hours. Nosotros volition take just the pollution variable as output at the following hour, every bit follows:

. . .

# divide into input and outputs

n_obs = n_hours * n_features

train_X , train_y = railroad train [ : , : n_obs ] , train [ : , - n_features ]

test_X , test_y = test [ : , : n_obs ] , exam [ : , - n_features ]

print ( train_X . shape , len ( train_X ) , train_y . shape )

Next, we can reshape our input data correctly to reverberate the fourth dimension steps and features.

. . .

# reshape input to exist 3D [samples, timesteps, features]

train_X = train_X . reshape ( ( train_X . shape [ 0 ] , n_hours , n_features ) )

test_X = test_X . reshape ( ( test_X . shape [ 0 ] , n_hours , n_features ) )

Fitting the model is the aforementioned.

The only other pocket-size modify is in how to evaluate the model. Specifically, in how we reconstruct the rows with eight columns suitable for reversing the scaling operation to go the y and yhat back into the original scale and then that nosotros tin can calculate the RMSE.

The gist of the change is that nosotros concatenate the y or yhat column with the last seven features of the test dataset in order to inverse the scaling, as follows:

. . .

# invert scaling for forecast

inv_yhat = concatenate ( ( yhat , test_X [ : , - vii : ] ) , axis = 1 )

inv_yhat = scaler . inverse_transform ( inv_yhat )

inv_yhat = inv_yhat [ : , 0 ]

# invert scaling for actual

test_y = test_y . reshape ( ( len ( test_y ) , one ) )

inv_y = concatenate ( ( test_y , test_X [ : , - 7 : ] ) , axis = 1 )

inv_y = scaler . inverse_transform ( inv_y )

inv_y = inv_y [ : , 0 ]

Nosotros can tie all of these modifications to the to a higher place example together. The complete instance of multvariate time series forecasting with multiple lag inputs is listed beneath:

ane

eight

ten

fourteen

nineteen

twenty

xxx

forty

ninety

from math import sqrt

from numpy import concatenate

from matplotlib import pyplot

from pandas import read_csv

from pandas import DataFrame

from pandas import concat

from sklearn . preprocessing import MinMaxScaler

from sklearn . preprocessing import LabelEncoder

from sklearn . metrics import mean_squared_error

from keras . models import Sequential

from keras . layers import Dense

from keras . layers import LSTM

# catechumen serial to supervised learning

def series_to_supervised ( information , n_in = 1 , n_out = 1 , dropnan = True ) :

n_vars = i if type ( data ) is listing else information . shape [ 1 ]

df = DataFrame ( data )

cols , names = list ( ) , list ( )

# input sequence (t-north, ... t-i)

for i in range ( n_in , 0 , - 1 ) :

cols . append ( df . shift ( i ) )

names += [ ( 'var%d(t-%d)' % ( j + 1 , i ) ) for j in range ( n_vars ) ]

# forecast sequence (t, t+1, ... t+n)

for i in range ( 0 , n_out ) :

cols . suspend ( df . shift ( - i ) )

if i == 0 :

names += [ ( 'var%d(t)' % ( j + 1 ) ) for j in range ( n_vars ) ]

else :

names += [ ( 'var%d(t+%d)' % ( j + 1 , i ) ) for j in range ( n_vars ) ]

# put it all together

agg = concat ( cols , axis = 1 )

agg . columns = names

# drop rows with NaN values

if dropnan :

agg . dropna ( inplace = True )

return agg

# load dataset

dataset = read_csv ( 'pollution.csv' , header = 0 , index_col = 0 )

values = dataset . values

# integer encode direction

encoder = LabelEncoder ( )

values [ : , 4 ] = encoder . fit_transform ( values [ : , four ] )

# ensure all data is float

values = values . astype ( 'float32' )

# normalize features

scaler = MinMaxScaler ( feature_range = ( 0 , 1 ) )

scaled = scaler . fit_transform ( values )

# specify the number of lag hours

n_hours = 3

n_features = 8

# frame as supervised learning

reframed = series_to_supervised ( scaled , n_hours , i )

print ( reframed . shape )

# separate into train and test sets

values = reframed . values

n_train_hours = 365 * 24

train = values [ : n_train_hours , : ]

examination = values [ n_train_hours : , : ]

# separate into input and outputs

n_obs = n_hours * n_features

train_X , train_y = railroad train [ : , : n_obs ] , train [ : , - n_features ]

test_X , test_y = examination [ : , : n_obs ] , test [ : , - n_features ]

print ( train_X . shape , len ( train_X ) , train_y . shape )

# reshape input to be 3D [samples, timesteps, features]

train_X = train_X . reshape ( ( train_X . shape [ 0 ] , n_hours , n_features ) )

test_X = test_X . reshape ( ( test_X . shape [ 0 ] , n_hours , n_features ) )

impress ( train_X . shape , train_y . shape , test_X . shape , test_y . shape )

# design network

model = Sequential ( )

model . add ( LSTM ( 50 , input_shape = ( train_X . shape [ 1 ] , train_X . shape [ 2 ] ) ) )

model . add ( Dense ( 1 ) )

model . compile ( loss = 'mae' , optimizer = 'adam' )

# fit network

history = model . fit ( train_X , train_y , epochs = l , batch_size = 72 , validation_data = ( test_X , test_y ) , verbose = ii , shuffle = Imitation )

# plot history

pyplot . plot ( history . history [ 'loss' ] , label = 'train' )

pyplot . plot ( history . history [ 'val_loss' ] , label = 'test' )

pyplot . fable ( )

pyplot . show ( )

# make a prediction

yhat = model . predict ( test_X )

test_X = test_X . reshape ( ( test_X . shape [ 0 ] , n_hours* n_features ) )

# capsize scaling for forecast

inv_yhat = concatenate ( ( yhat , test_X [ : , - seven : ] ) , axis = 1 )

inv_yhat = scaler . inverse_transform ( inv_yhat )

inv_yhat = inv_yhat [ : , 0 ]

# invert scaling for actual

test_y = test_y . reshape ( ( len ( test_y ) , one ) )

inv_y = concatenate ( ( test_y , test_X [ : , - seven : ] ) , centrality = i )

inv_y = scaler . inverse_transform ( inv_y )

inv_y = inv_y [ : , 0 ]

# calculate RMSE

rmse = sqrt ( mean_squared_error ( inv_y , inv_yhat ) )

print ( 'Test RMSE: %.3f' % rmse )

Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average event.

The model is fit as earlier in a infinitesimal or ii.

...

Epoch 45/50

1s - loss: 0.0143 - val_loss: 0.0154

Epoch 46/fifty

1s - loss: 0.0143 - val_loss: 0.0148

Epoch 47/50

1s - loss: 0.0143 - val_loss: 0.0152

Epoch 48/50

1s - loss: 0.0143 - val_loss: 0.0151

Epoch 49/50

1s - loss: 0.0143 - val_loss: 0.0152

Epoch 50/50

1s - loss: 0.0144 - val_loss: 0.0149

A plot of train and test loss over the epochs is plotted.

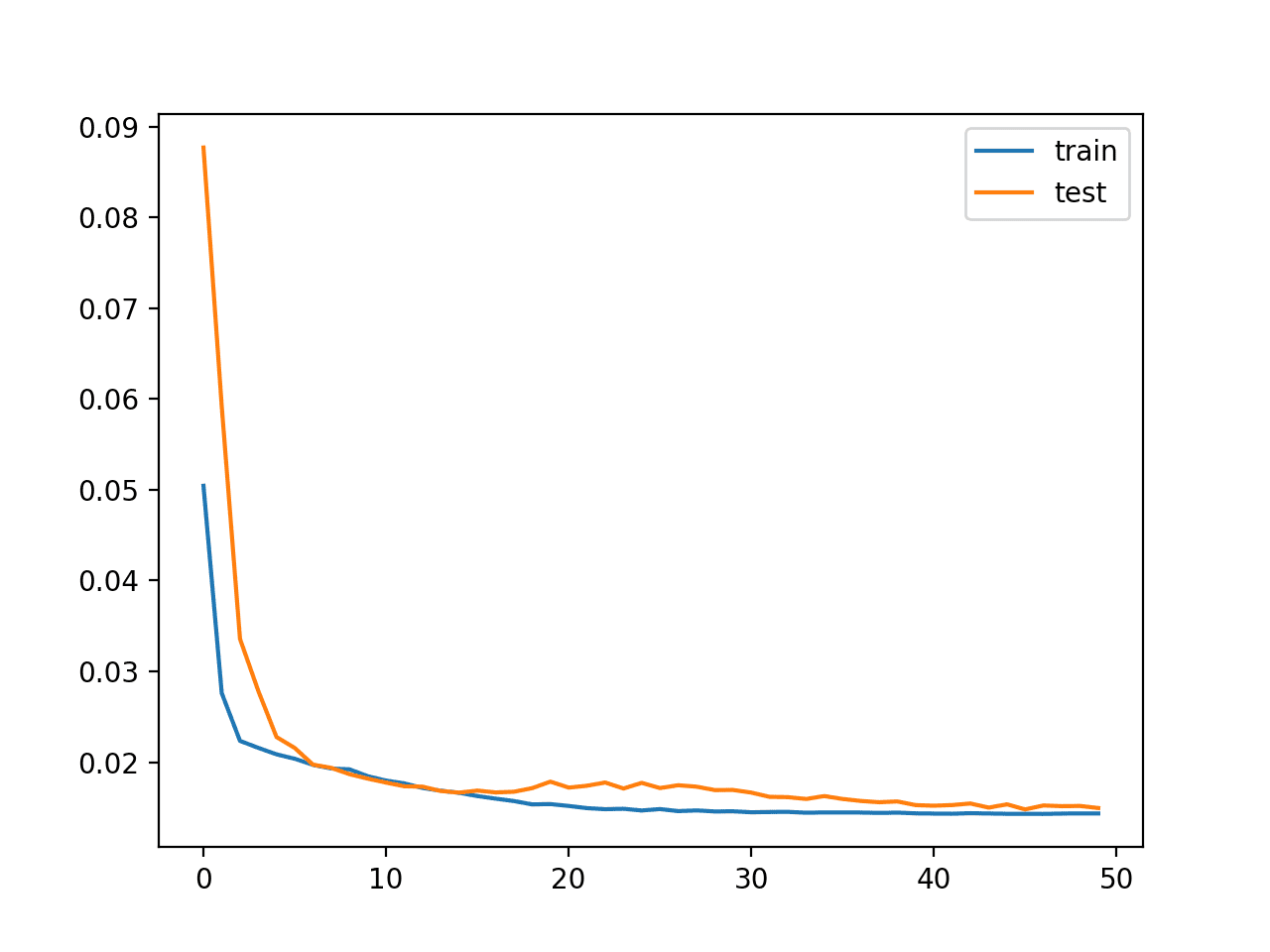
Plot of Loss on the Railroad train and Exam Datasets

Finally, the Test RMSE is printed, not actually showing any advantage in skill, at least on this problem.

I would add that the LSTM does not appear to be suitable for autoregression blazon problems and that you may be better off exploring an MLP with a large window.

I hope this example helps you lot with your own time series forecasting experiments.

Summary

In this tutorial, you discovered how to fit an LSTM to a multivariate fourth dimension series forecasting problem.

Specifically, you learned:

How to transform a raw dataset into something we can use for time serial forecasting.
How to gear up data and fit an LSTM for a multivariate time series forecasting trouble.
How to make a forecast and rescale the outcome back into the original units.

Do you lot have whatever questions?
Ask your questions in the comments below and I will do my best to reply.

Develop Deep Learning models for Fourth dimension Serial Today!

Develop Your Own Forecasting models in Minutes

...with only a few lines of python code

Find how in my new Ebook:
Deep Learning for Time Series Forecasting

It provides cocky-study tutorials on topics like:
CNNs, LSTMs, Multivariate Forecasting, Multi-Footstep Forecasting and much more...

Finally Bring Deep Learning to your Time Series Forecasting Projects

Skip the Academics. Merely Results.

Come across What'south Within